Dans toutes les oeuvres de cette rubrique, le carré est une brique élémentaire qui sert à construire des damiers carrés ou rectangulaires. Les cellules de ces damiers vont ensuite recevoir un contenu (signe, couleur) qui sera visible. Les traits qui séparent les cellules ne sont pas modifiés et restent neutres, voire même invisibles comme dans les "
répartitions TCC". Ces acryliques sur papier sont des oeuvres anciennes, dans lesquelles un tableau de 72 cases reçoit 6 sortes de signes : des triangles, des carrés ou des cercles (d'où le titre TCC) qui sont noirs ou rouges. Les signes sont répartis de manière aléatoire, mais avec des contraintes d'équilibre.
Les "
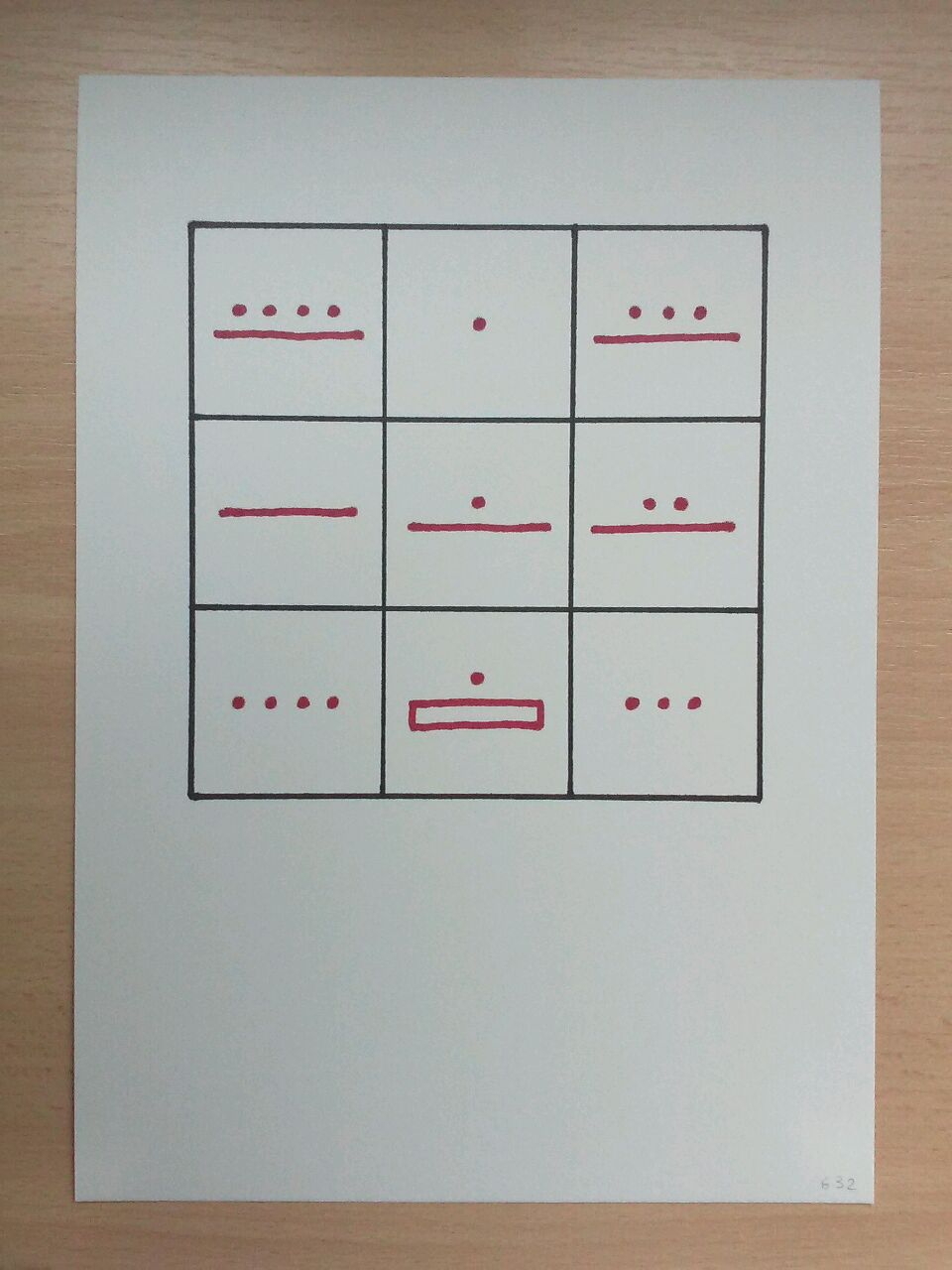
carrés aléatoires" sont construits sur le même principe ; la différence est que toutes les cases du damier ne sont pas remplies, et que les signes qui sont tracés dans certaines cellules sont des nombres tirés au hasard, représentés selon un système personnel inspiré de la numération maya.
Cette numération maya se retrouve dans les "carrés magiques", petite série de 16 dessins consacrée aux carrés magiques 3x3, de base 15 à 30.
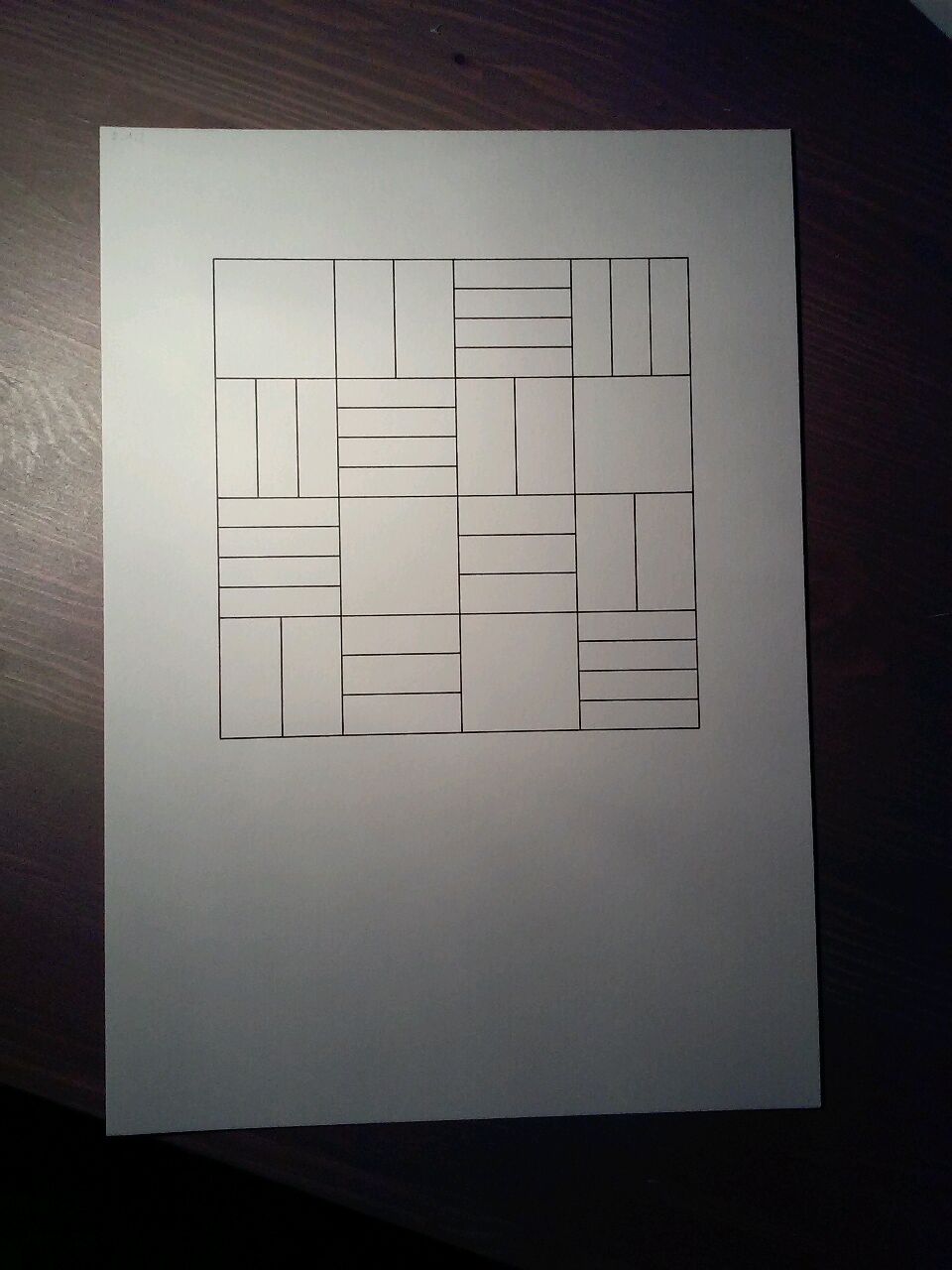
Les "mini-sudokus" sont comme leur nom l'indique, des sudokus à 16 cases, qui ne contiennent donc que les chiffres de 1 à 4. Chaque chiffre est ici représenté par le nombre de divisions dans sa case. Les divisions sont alternativement horizontales et verticales pour éviter de "transpercer" les cloisons du tableau. Le projet vise en outre à inventorier toutes les formes possibles (il y en a 288) ; en tenant compte des rotations, il comprend 78 dessins.
Les "
inventaires" obéissent au même désir d'épuiser la richesse combinatoire d'un ensemble de règles ; ici il s'agit simplement de noircir des cases d'un damier et de faire le tour des possibilités, en tenant compte des rotations et des mises en miroir.
Le "
catalogue des formes contraintes" dérive directement de ces inventaires ; les formes conservées obéissent à certaines contraintes (nombre d'éléments, géométrie, topologie) et leur coloration varie selon leur nombre d'éléments (qui sépare les formes blanches des formes colorées) et leur topologie (formes noires, rouges, jaunes ou bleues).